配对交易简介
配对交易是指八十年代中期华尔街著名投行Morgan Stanley的数量交易员Nunzio Tartaglia成立的一个数量分析团队提出的一种市场中性投资策略,,其成员主要是物理学家、数学家、以及计算机学家。
Ganapathy Vidyamurthy在《Pairs Trading: Quantitative Methods and Analysis》一书中定义配对交易为两种类型:一类是基于统计套利的配对交易,一类是基于风险套利的配对交易。
基于统计套利的配对交易策略是一种市场中性策略,具体的说,是指从市场上找出历史股价走势相近的股票进行配对,当配对的股票价格差(Spreads)偏离历史均值时,则做空股价较高的股票同时买进股价较低的股票,等待他们回归到长期均衡关系,由此赚取两股票价格收敛的报酬。
数据分析
数据来自交易所:币安,数据下载可以关注Python 视界,发送 配对交易 即可获取下载地址。

数据包括几种常见数据货币每个小时的价格,每一种数字火币的交易记录有 20000条。
如下图所示:
具体的数据如下图所示:

数据处理
因为每种数字货币的价格不一样,为了体现出他们的关联性,首先要进行归一化操作,将价格归一化处理。这里采用的是 sklearn 中的 MinMaxScaler。
## 节选代码
from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler()
np_list=np.asarray(data_items).reshape(-1,1)
X_train_minmax = min_max_scaler.fit_transform(np_list)
归一化之后,基于 matplotlib 进行可视化
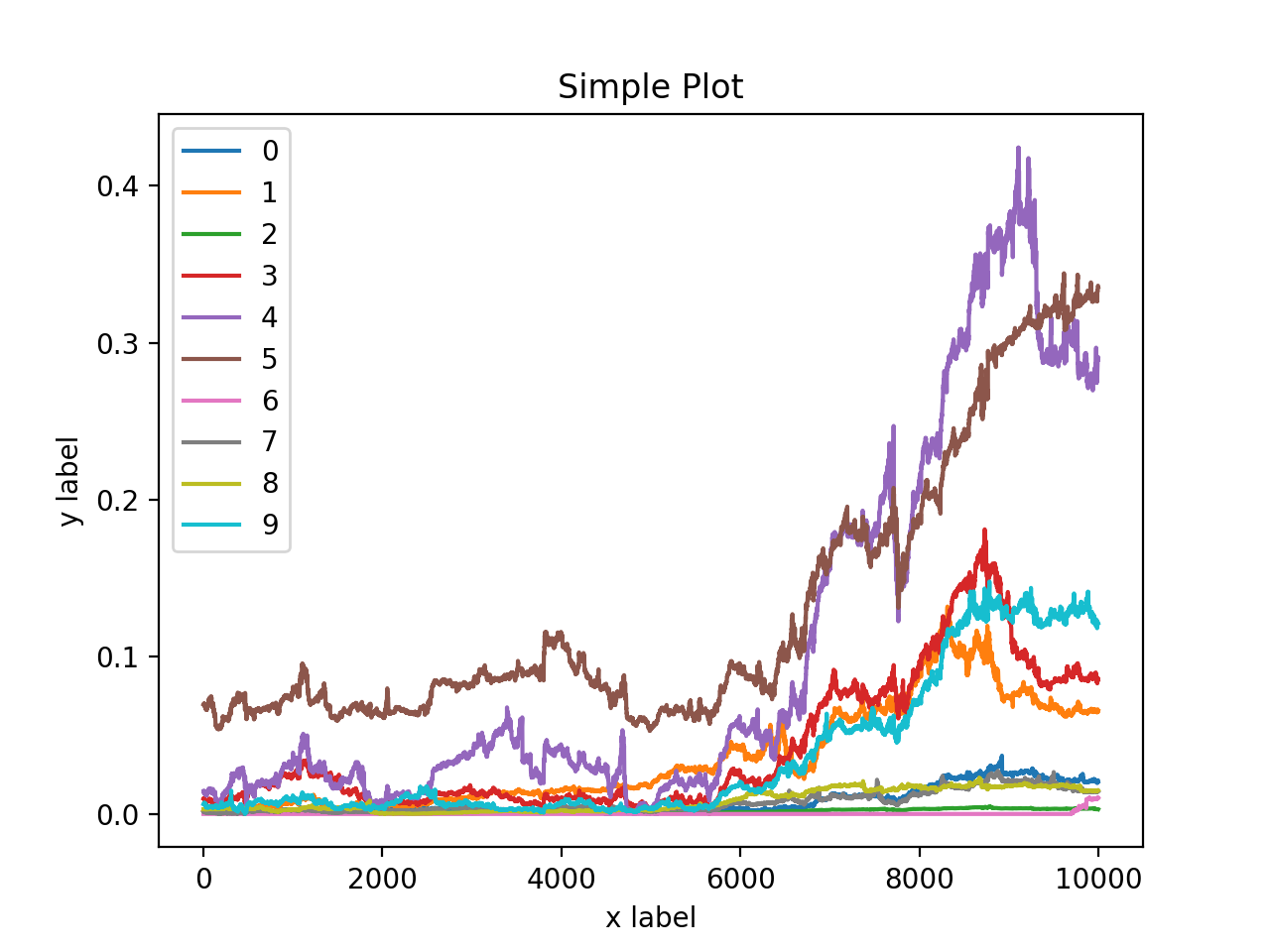
肉眼可见,最上面两个曲线之间有一定的关联性,两者在分离之后多次汇合,接下来借助协方差来评估二者之间的关联度。
模型实现
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
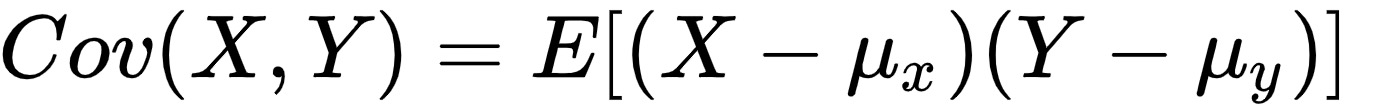
采用 numpy 中的 cov 函数来实现协方差的计算。
import numpy as np
np.cov(x,y)
输出样例:
[[ 9.44749900e-09 -4.05910662e-09]
[-4.05910662e-09 3.38730102e-08]]
效果评估
4个数字货币的交易记录
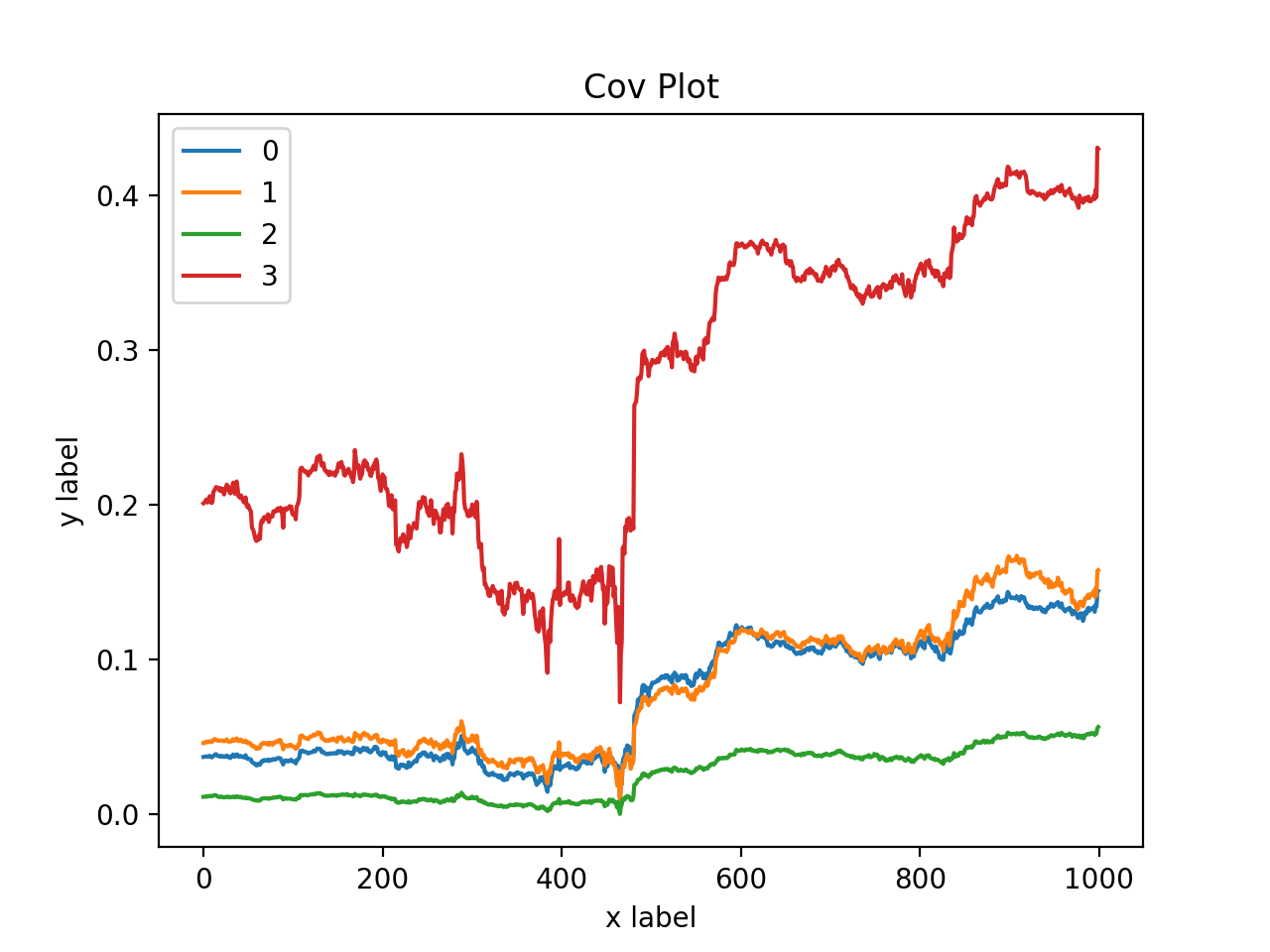
其中 0,1 之间有很高的关联度
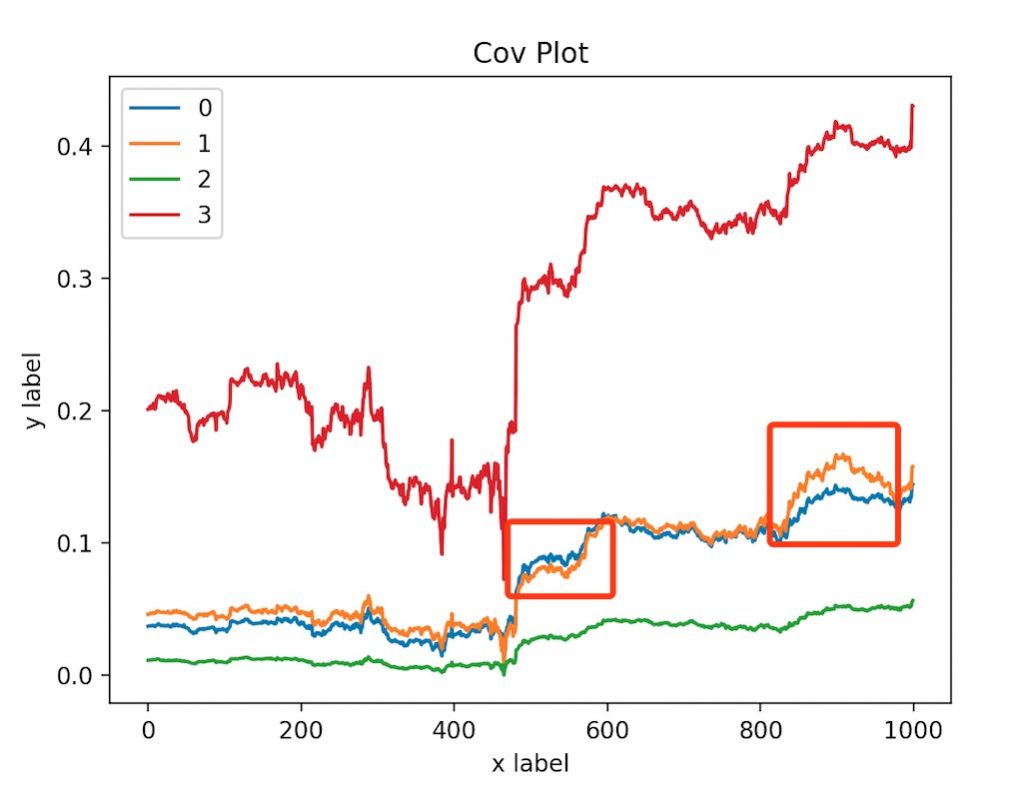
可以在两个价格分离的时候,买入低价的A,卖出高价的B,当二者价格重新回归的时候平仓,即可以获得盈利。
相关知识
配对交易:https://wiki.mbalib.com/wiki/%E9%85%8D%E5%AF%B9%E4%BA%A4%E6%98%93
币安:https://www.binance.com/cn/register?ref=23297069
协方差:https://www.zhihu.com/question/20852004
相关教程
sklearn:http://sklearn123.com/
Python:http://pythonok.com/
Pytorch:http://pytorch123.com/
未经允许不得转载:PythonOK » 配对交易-低风险统计套利量化交易 Python 实战

 PythonOK
PythonOK 币安比特币交易所涨幅榜 日榜2021-06-01
币安比特币交易所涨幅榜 日榜2021-06-01
 【Python教程】《零基础入门学习Python》最新版(小甲鱼)
【Python教程】《零基础入门学习Python》最新版(小甲鱼) 玩转年薪50W从零基础到量化工程师进阶篇
玩转年薪50W从零基础到量化工程师进阶篇 PythonABC 小伙伴们,跟我一起从零开始学Python吧
PythonABC 小伙伴们,跟我一起从零开始学Python吧